Question

Calculate the moment of inertia of a 60.0kg skater with her arms sticking straight out. the skater’s torso and legs are approximated as a cylinder that has a 0.110-m radius. her two arms are 0.900 m long and are 3.75 kg each.

Answer 1

The moment of inertia of the skater is calculated by approximating the body as a cylinder and the arms as rods rotating about one end, resulting in a total moment of inertia of 2.3426 kg*m² .

Step-by-step explanation:

To calculate the moment of inertia of the skater, we need to consider her body and arms separately.

The body is approximated as a cylinder, and the arms are approximated as rods rotating about one end.

The moment of inertia for a cylinder (Icylinder) is given by Icylinder = (1/2) * mcylinder * r² where mcylinder is the mass of the cylinder and r is the radius.

For the arms, treated as rods, the moment of inertia (Iarm) is Iarm = (1/3) * marm * L² where marm is the mass of an arm and L is the length of the arm.

Given the mass of the cylinder as 52.5 kg and the mass of each arm as 3.75 kg:

• Icylinder = (1/2) * 52.5 kg * (0.110 m)² = 0.3176 kg*m²
• Iarm = (1/3) * 3.75 kg * (0.900 m)² = 1.0125 kg*m² per arm

Since the skater has two arms, the total moment of inertia for the arms is
`2 * Iarm.`

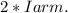
The total moment of inertia of the skater is the sum of Icylinder and the moments of inertia for both arms:

Total I = Icylinder + 2 * Iarm = 0.3176 kg*m² + 2 * 1.0125 kg*m ² = 2.3426 kg*m²