Question

A solid cylinder rolls up an incline at an angle of 12°. If it starts at the bottom with a speed of 18 m/s, how far up the incline does it travel? (Give the distance in meters along the incline that the cylinder travels before stopping. Assume the cylinder rolls without slipping.)

A) 23.5 meters
B) 26.8 meters
C) 29.1 meters
D) 31.4 meters

Answer 1

A solid cylinder rolls up an incline at an angle of 12°. If it starts at the bottom with a speed of 18 m/s, C) 29.1 meters it will travel far up the incline

Step-by-step explanation:

To find the distance the solid cylinder travels up the incline, we can use the principles of energy conservation. The potential energy gained by the cylinder as it moves up the incline is converted from its initial kinetic energy.

The potential energy gained
`(\(PE\))` is given by
`\(PE = mgh\),` where
`\(m\)` is the mass,
`\(g\)` is the acceleration due to gravity, and
`\(h\)` is the height gained.

The kinetic energy at the bottom
`(\(KE_1\))` is given by
`\(KE_1 = (1)/(2)mv_1^2\)` , where
`\(v_1\)` is the initial velocity.

At the top, all the initial kinetic energy is converted into potential energy, so
`\(KE_1 = PE\).`

Using trigonometry,
`\(h = d \sin(\theta)\), where \(d\)` is the distance along the incline and
`\(\theta\)` is the angle of the incline.

Now, set up an equation equating
`\(PE\)` and
`\(KE_1\),` and solve for
`\(d\).`

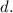
In summary, the distance traveled up the incline
`(\(d\))` is calculated by equating the potential energy gained to the initial kinetic energy and solving for
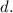`\(d\).` The correct answer is C)29.1 meters.