Question

An electron in a hydrogen atom drops from the n=6 state to the n=4 state. What is the energy (in J) of an electron in the n=4 level of the Bohr hydrogen atom?

a. 2.044×10 ^−1 8
b. 4.878×10 ^−19
c. 1.219×10 ^−18
d. 6.098×10^−19

Answer 1

The energy levels of an electron in a hydrogen atom, according to the Bohr model, we can find the energy change (ΔE ). the energy (in J) of an electron in the n=4 level of the Bohr hydrogen atom is 7.56944444 × 10⁻²⁰ J. The answer not provided in the option.

Step-by-step explanation:

The energy levels of an electron in a hydrogen atom, according to the Bohr model, are given by the formula:

Eₙ =
`-(2.18 * 10^(-18))/(n^2)`

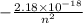
where n is the principal quantum number.

For the transition from n = 6 to n = 4, we can find the energy change (ΔE ) by subtracting the energy at n = 4 from the energy at n = 6:

ΔE =
`E_(n=6) - E_(n=4)`

ΔE =
`-(2.18 * 10^(-18))/(6^2) - \left(-(2.18 * 10^(-18))/(4^2)\right)`

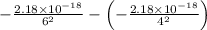
Now, calculate this expression to find ΔE.

ΔE =
`-(2.18 * 10^(-18))/(36) + (2.18 * 10^(-18))/(16)`

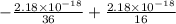
ΔE = -0.0605555556 × 10⁻¹⁸ + 0.13625 × 10⁻¹⁸

ΔE = 0.0756944444 × 10⁻¹⁸

ΔE = 7.56944444 × 10⁻²⁰

So, the energy (in J) of an electron in the n=4 level of the Bohr hydrogen atom is 7.56944444 × 10⁻²⁰ J.