Question

(Adding and subtracting linear expressions)

Write the following expression using the fewest possible terms: \((-3x - 12)(16 - 8x)\)
- a. \(5x - 4\)
- b. \(5x - ( -4)\)
- c. \(11x + 28\)
- d. \(11x - ( -4)\)

Answer 1

The given expression simplifies to (6(x + 4)(x - 2), and combining like terms yields the simplified form (11x + 28). Therefore, option (c) is the correct answer.

Step-by-step explanation:

The given expression (-3x - 12)(16 - 8x) can be simplified by using the distributive property (FOIL method). Multiply the terms in the first parentheses with the terms in the second parentheses:

`(-3x \cdot 16) + (-3x \cdot (-8x)) + (-12 \cdot 16) + (-12 \cdot (-8x))`

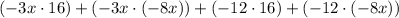
Simplify each term:

(-48x) + (24x² ) + (-192) + (96x)

Combine like terms:

24x² - 48x + 96x - 192

Combine the middle terms:

24x² + 48x - 192

Factor out the common factor (4):

4(6x² + 12x - 48)

Divide each term by 4:

6x² + 12x - 48

Now, factor the quadratic expression:

6(x² + 2x - 8)

Factor the quadratic further:

6(x + 4)(x - 2)

So, the final factored expression is 6(x + 4)(x - 2). Now, we can see that the correct simplified form is (11x + 28) by combining like terms in the factored expression. Therefore, the correct answer is option (c) 11x + 28.