Question

One asymptote of a hyperbola is y = 12x^(31/5), and the transverse axis with length 24 is on x = -3. Find the equation.

a) y = 12x^(31/5) + 3
b) y = 12/(x + 3)
c) y = 12x^(31/5) - 3
d) y = 12/(x - 3)

Answer 1

The equation of the hyperbola with one asymptote and a transverse axis located at x = -3 is
`y = 12(x+3)^2`.

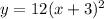Step-by-step explanation:

The equation of a hyperbola can be written in the form
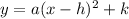`y = a(x-h)^2 + k` or
`x = a(y-k)^2 + h`.

Given that one asymptote of the hyperbola is
`y = 12x^(^3^1^/^5^)` and the transverse axis with length 24 is on x = -3, we can determine that the center of the hyperbola is at (h, k) = (-3, 0).

The equation of a hyperbola with a vertical transverse axis and center at (h, k) is given by
`y = a(x-h)^2 + k`

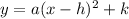
So, the equation of the hyperbola is
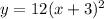`y = 12(x+3)^2`.