Question

I need help explaining how to get the answer for this question.

Answer 1

a. Ben has a higher rate of memorization.

b. Ben memorizes 0.006t more words from t=0 to t=10.

c. On average, Alice memorizes −0.018t+0.4 words per minute.

d. On average, Ben memorizes 0.006 words per minute.

a) To determine who has the higher rate of memorization, compare the coefficients of the quadratic and linear terms in the functions. In Ben's function,
`\(M(t) = 0.003t + 0.4t\)`, the coefficient of the highest degree term (t) is positive (0.003), indicating a positive rate of memorization. In Alice's function,
`\(m(t) = -0.009t^2 + 0.4t\)`, the coefficient of the highest degree term (\(t^2\)) is negative (-0.009), indicating a negative rate of memorization. Since a positive rate implies a better memorization rate, Ben has a higher rate of memorization.

b) To find the difference in the number of words memorized from \(t = 0\) to \(t = 10\), subtract Alice's memorization function from Ben's:

`\[M(t) - m(t) = (0.003t + 0.4t) - (-0.009t^2 + 0.4t)\`

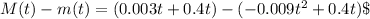
Simplifying, we get \(0.006t\), which represents the additional words Ben memorizes compared to Alice over the given time interval.

c) To find the average rate of memorization for Alice over the first 10 minutes, calculate the average rate by taking the derivative of her memorization function \(m(t)\) with respect to \(t\):

`\[m'(t) = (d)/(dt)(-0.009t^2 + 0.4t)\]`

Simplifying, we get \(-0.018t + 0.4\), representing the average rate of memorization for Alice.

d) Similarly, find the average rate of memorization for Ben over the first 10 minutes by taking the derivative of his memorization function \(M(t)\) with respect to \(t\):

`\[M'(t) = (d)/(dt)(0.003t + 0.4t)\]`

Simplifying, we get \(0.006\), representing the average rate of memorization for Ben.