Question

Solve the system of equations by substitution. Show all work neatly on your work page. Checking your work is wise. :)

3x + 2y = -10

y = -5x + 9

Answer 1

(4, -11)

Explanation:

We are given the system of equations:

`\displaystyle \begin{cases} 3x+2y=-10\\ y=-5x+9\end{cases}`

And we want to solve by substitution.

Notice that y is isolated in the second equation.

Therefore, we can substitute the second equation into the first. This gives us:

`3x+2(-5x+9)=-10`

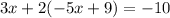
Now, we can solve for x.

First, distribute:

`\displaystyle 3x-10x+18=-10`

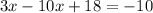
Next, we can combine like terms:

`-7x+18=-10`

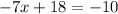
Subtract 18 from both sides:

`-7x=-28`

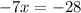
And divide both sides by -7:

`x=4`

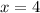
So, the value of x is 4.

Using the second equation then, we can solve for y:

`y=-5x+9`

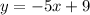
Since we know that x = 4:

`\displaystyle y = - 5(4) + 9 = -20 + 9 = -11`

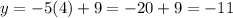
So, our solution is (4, -11).

To check, we can simply substitute the x and y values and see if the two equations are true.

For the first equation:

`3(4)+2(-11)=12-22=-10\stackrel{\checkmark}{=}-10`

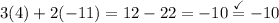
And for the second equation:

`-5(4)+9=-20+9=-11\stackrel{\checkmark}{=}-11`

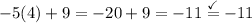
Since both statements are true, (4, -11) is indeed correct!