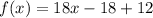Answer:
 --- Function A
--- Function A
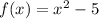 --- Function B
--- Function B
 --- Function C
--- Function C
Explanation:
Solving (a): Equation of Function A
An exponential equation is represented as:
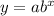
From the graph of function A,
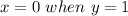
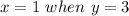
For:
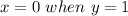
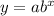 becomes
becomes
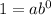
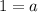
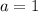
For:
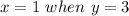
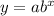 becomes
becomes

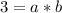
Substitute 1 for a
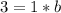
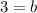
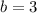
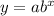 becomes
becomes
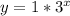
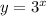
Replace y with f(x)

Solving (b): Equation of Function B
A quadratic equation is represented as:
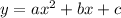
From the table of function B,
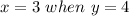
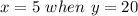
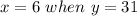
For:
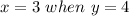
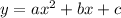 becomes
becomes
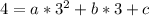
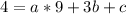
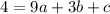
For
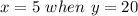
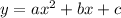 becomes
becomes
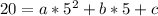
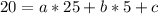
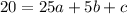
For
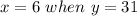
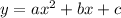 becomes
becomes
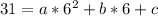
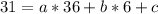
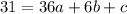
So, we solve for a, b and c in:
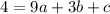
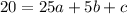
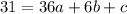
Make c the subject in
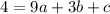
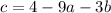
Substitute
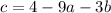 in
in
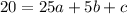 and
and
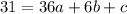
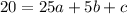 becomes
becomes
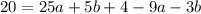
Collect Like Terms
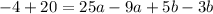

Divide through by 2
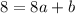
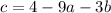
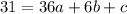 becomes
becomes
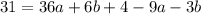
Collect Like Terms
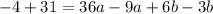
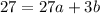
Divide through by 3
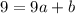
Solve for a and b in:
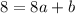 and
and
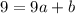
Subtract both equations:
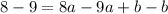
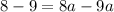
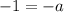
Divide both sides by -1
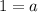
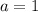
Substitute 1 for a in
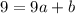
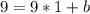
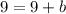
Subtract 9 from both sides
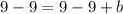
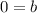
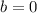
Substitute
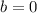 and
and
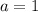 in
in
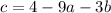
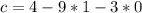

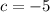
So, the equation is:
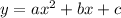
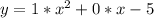

Replace y with f(x)
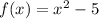
Solving (c): Equation of Function C
This is calculated using:
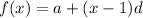
Where
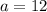 -- the first term
-- the first term
d = the difference between successive terms

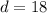
So, we have:
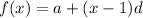
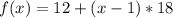
Open bracket
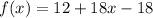
Collect Like Terms