Question

Angel earned a score of 174 on Exam A that had a mean of 150 and a standarddeviation of 40. He is about to take Exam B that has a mean of 550 and a standarddeviation of 40. How well must Angel score on Exam B in order to do equivalentlywell as he did on Exam A? Assume that scores on each exam are normally distributed.

Answer 1

We need to calculate first for the z-score of Angel on Exam A. The z-score can be computed using the equation:

Given the mean, score (represented by x), and the standard deviation, Angel's z-score in exam A is computed as follows:

`\begin{gathered} z=(174-150)/(40) \\ z=(24)/(40)=0.6 \end{gathered}`

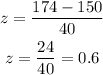
We now derive an equation solving for x to compute the needed score of Angel on Exam B so that she has the same performance as Exam A.

Using the z score computed on Exam A plus the mean and standard deviation for Exam B, the minimum points Angel needed will be:

`\begin{gathered} z=(550)+(0.6\cdot40) \\ z=550+24=574 \end{gathered}`

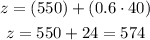
Therefore, Angel needs a score of 574 on exam B so that he can do equivalently as well as Exam A.

Answer: 574 points