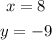1 Answer

Sharhabeel Hamdan · Answer 1 · 2023-01-27T06:30:56+0000

To solve the system of equations:

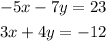
$\begin{gathered} -5x-7y=23 \\ 3x+4y=-12 \end{gathered}$

We can do by adding equations. To do that, we need to make the coefficient of one of the variables the same but with different signs.

We can do that with x by multiplying the first equations by 3 and the second by 5:

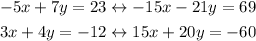
$\begin{gathered} -5x+7y=23\leftrightarrow-15x-21y=69 \\ 3x+4y=-12\leftrightarrow15x+20y=-60 \end{gathered}$

Now, we add them:

$\begin{gathered} -15x-21y=69 \\ 15x+20y=-60 \\ 0x-1y=9 \\ -y=9 \\ y=-9 \end{gathered}$

Now, we can substitute y into either equation to find out x:

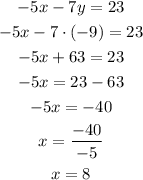
$\begin{gathered} -5x-7y=23 \\ -5x-7\cdot(-9)=23 \\ -5x+63=23 \\ -5x=23-63 \\ -5x=-40 \\ x=(-40)/(-5) \\ x=8 \end{gathered}$

So, the solution is:

$\begin{gathered} x=8 \\ y=-9 \end{gathered}$

Your comment on this question: