Question

if the point (-1,4)and (2,13)are on the graph of the quadratic function
`y = 7x {}^(2) + bx + c`what are the values of b and c

Answer 1

The Solution:

Given:

`y=7x^2+bx+c`

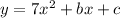
Given that the points: (-1,4) and (2,13) are on the graph of the given equation,

We are required to find the values of a and b.

Substitute (x= -1, y = 4) in the equation, we get:

`\begin{gathered} 4=7(-1)^2+b(-1)+c \\ 4=7-b+c \\ -3=-b+c...eqn(1) \end{gathered}`

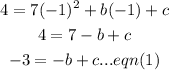
Substitute (x= 2, y = 13) in the equation, we get:

`\begin{gathered} 13=7(2)^2+b(2)+c \\ 13=28+2b+c \\ -15=2b+c...eqn(2) \end{gathered}`

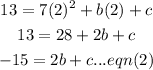
Solving eqn(1) and eqn(2) simultaneously by the elimination method:

Subtract eqn(1) from eqn(2):

`\begin{gathered} -15--3=2b--b+c-c \\ -12=3b \end{gathered}`

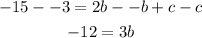
Divide both sides by 3.

`b=(-12)/(3)=-4`

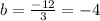
Substitute -6 for b in eqn(1).

`\begin{gathered} -3=-b+c \\ -3=-(-4)+c \\ \\ -3=4+c \\ -3-4=c \\ -7=c \\ c=-7 \end{gathered}`

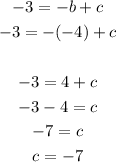
Therefore, the correct answers are:

b = -4

c = -7