Question

For each of the following sequences (either arithmetic or geometric), find a possible function f(n) whose domain is the set of natural numbers and whose outputs are the terms of the sequence.a. 4, 8, 12, 16, 20, ...b. 1, 4, 16, 64, 256, ...c. √3, √3, √3, √3, ...

Answer 1

Sequence a: 4, 8, 12, 16, 20, ...

As you can observe, this is an arithmetic sequence with a difference of 4 because each new term is 4 units more than the previous one: 4+4=8, 8+4=12, 12+4=16,...

We have to use the function for arithmetic sequences

`f(n)=f(1)+(n-1)\cdot d`

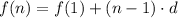
Where f(1) = 4 and d = 4. So, the function is

`f(n)=4+(n-1)\cdot4=4+4n-4=4n`

Hence, the function of the sequence a is f(n) = 4n.

Sequence b: 1, 4, 16, 64, 256, ...

This sequence is geometric because each new term is four times its previous one: 1x4=4, 4x4=16, 16x4=64,...

We have to use the function for geometric sequences

`f(n)=f(1)\cdot r^(n-1)_{}`

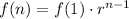
Where f(1) = 1 and r = 4.

`f(n)=1\cdot(4)^(n-1)`

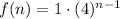
Hence, the function is

`f(n)=4^(n-1)`

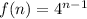
Sequence c.

As you can observe, this sequence is formed by the same number, which means it represents a constant function like the following

`f(n)=\sqrt[]{3}`