Question

Please teach me how to get Dimensions from those quantity and dimensional equivalent

Answer 1

We need to do a dimensional analysis of the dimensions of force.

We need to have into account what the following symbols represent:

`\begin{gathered} M=\text{ mass} \\ L=\text{ length} \\ T=\text{ time} \end{gathered}`

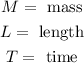
In the case of force, we look into the table and we notice that the dimension column says:

`MLT^(-2)`

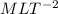
The negative exponent can be brought down as follows:

`(ML)/(T^2)`

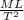
This means that any force has units of "mass" multiplied by "length" divided by "time squared". In the International System (SI) this unit is equivalent to Newtons (N). Newtons in the international system is equivalent to:

`kg(m)/(s^2)`

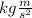
Where:

`\begin{gathered} kg=\text{ kilograms} \\ m=\text{ meters} \\ s=\text{ seconds} \end{gathered}`

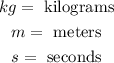
We notice that "kg" is mass, "m" is length, and "s" is time. Therefore, these units are consistent with the dimensions of the units of force.

When doing a dimensional analysis we need to substitute the dimensions we are using to get equivalent dimensions. For example:

`(J)/(m)`

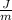
These units are Joule divided by meters. Now, we substitute the dimensions of Joules and the dimensions of meters:

`(J)/(m)=(ML^2T^(-2))/(L)`

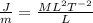
We can cancel out the length "L":

`(J)/(m)=MLT^(-2)`

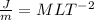
We notice that the units are equivalent to the units of force:

`(J)/(m)=N`

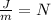
Therefore, Joules divided by meters is Newtons.