Question

the point Q lies on the curve f(x) = -x^2 + 6x-7 and has coordinates (4,1)Line L, through Q, is perpendicular to the tangent at Qa) Calculate the gradient of Lb) find the equation of Lc) The line intersects the curve again at R. Find the coordinates of R2. Find the coordinates of the point on the graph of f(x) = x^2-x at which the tangent is parallel to the line y=5x

Answer 1

Step 1: Write out the function

`f(x)=-x^2+6x-7^{}`

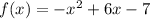
Step 2: Differentiate the function in step 1 with respect to x

`f^(\prime)(x)=-2x+6`

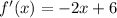
Step 3: Find the gradient, n, of the tangent line through Q.

the gradient of the tangent line throught Q is given by the value of f'(x) at the point (4,1)

`\begin{gathered} \text{ In this case,} \\ x=4 \\ \text{ Therefore} \\ n=f^(\prime)(4)=-2(4)+6=-8+6=-2 \end{gathered}`

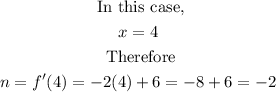
Step 4 (a): Find the gradient of the line L.

Since line L is perpendicular to the tangent line of Q, then the gradient, m, of the line L is given by

`\begin{gathered} m=-(1)/(n) \\ \text{ Thus} \\ m=-(1)/(-2)=(1)/(2) \end{gathered}`

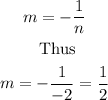
Step 5: Write out the formula for finding the equation of a line through the point (x1,y1)

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{ wh}ere \\ m\text{ is the gradient of the line} \end{gathered}`

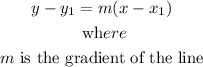
Step 6 (b): Find the equation of line L

`\begin{gathered} y-1=(1)/(2)(x-4) \\ y=(x)/(2)-1 \end{gathered}`

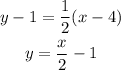
Hence the equation of line L is: y = 1/2 x - 1

Step 7 (c): Find the coordinates of R

At R, line L intersects the curve.

Therefore,

`\begin{gathered} -x^2+6x-7=(1)/(2)x-1 \\ The\text{ refore} \\ x^2-(11)/(2)x+6=0 \\ (x-(11)/(4))^2-(-(11)/(4))^2+6=0 \\ (x-(11)/(4))^2=(25)/(16) \\ x-(11)/(4)=\pm(5)/(4) \\ x=(11+5)/(4),(11-5)/(4)=4,(3)/(2) \end{gathered}`

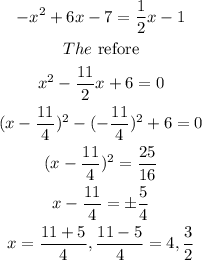
at x = 3/2

`f((3)/(2))=4.25`

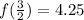
Hence, the coordinates of R is (3/2, 4 1/4)