Question

Which are the center and radius of the circle with equation (x+5)^2+ (y-4)^2= 9?

Answer 1

The general equation of a circle is:

`(x-a)^2+(y-b)^2=r^2`

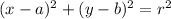
where:

(a, b) = coordinates of the center of the circle

r = radius of the circle

Now, the equation given in the question, which is:

`(x+5)^2+(y-4)^2=9`

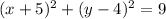
Can be re-written as follows:

`\begin{gathered} (x+5)^2+(y-4)^2=9 \\ \Rightarrow(x-(-5))^2+(y-4)^2=3^2 \end{gathered}`

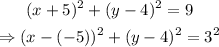
Now, we can easily compare the resulting expression with the general equation of a circle.

On doing so, we have that:

(a, b) = (-5, 4)

r = 3

Thus, the center of the circle is (-5, 4) and the radius is 3

Therefore, the correct answer is: Option C