Given:
The first type is 20% pure fruit juice, and the second type is 70% pure fruit juice.
To find:
The amount in pints of each of the existing types of drink must be used to make 70 pints of a mixture that is 35% pure fruit juice.
Step-by-step explanation:
Let x be the number of pints in the first type.
Let y be the number of pints in the second type.
According to the problem,

Multiply equation (1) by 0.2, and we get
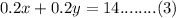
Subtract (3) from (2), we get,
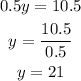
Substituting into equation (1) we get,
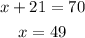
Final answer:
• First fruit drink: 49 pints
,
• Second fruit drink: 21 pints