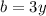Question:
Solution:
Consider the following expression:
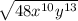
Applying the properties of radicals, we get:
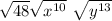
now, this is equivalent to:
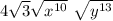
this is equivalent to:
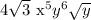
this is equivalent to:
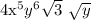
finally, applying the properties of radicals, we get:
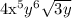
Answer: we can conclude that the correct answer is:
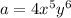
and