Question

Bank On ItAn investor has $5000 to invest for 10 years in one of thebanks listed below. Each bank offers an interest rate that iscompounded annually.BankPrincipal Years BalanceSuper Save $10006 $1173.34Star Financial $2500 3 $2684.35Better Bank $4000 5 $4525.63The investor chooses Better Bank because it earned over $100per year, which is much more than the other banks earned per year.1. a graph showing how the investment would grow over a 10-year period, and2. the interest rate, including how you found it.Be creative in your presentation. Remember, you want to convince an investor whichbank is the best choice! I only need help with the graph part

Answer 1

EXPLANATION

First, we need to apply the compounding interest equation as given below:

`A=P(1+(r)/(n))^(nt)`

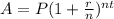
Where A=balance, P=principal, r=interest rate, n=number of times interest rate is compounded (in this case the interest rate is compounded annually, so n=1)

First, we need to isolate the interest rate from each bank.

Isolating r from the Compounding interst equation:

(Dividing both sides by P):

`(A)/(P)=(1+(r)/(n))^(nt)`

Applying the nt root to both sides:

`\sqrt[nt]{(A)/(P)}=(1+(r)/(n))`

Removing the parentheses:

`\sqrt[nt]{(A)/(P)}=1+(r)/(n)`

Subtracting -1 to both sides:

`\sqrt[nt]{(A)/(P)}-1=(r)/(n)`

Multiplying both sides by n. As n=1 we can desestimate this step.Additionally, as n=1 --> nt=1*t = t

`\sqrt[t]{(A)/(P)}-1=r`

Switching sides:

`r=\sqrt[t]{(A)/(P)}-1`

Now we can compute the interest rate for each bank as follows:

`r_{Super\text{ Save}}=\sqrt[6]{(1173.34)/(1000)}-1`
`r_{\text{Super Save}}=\sqrt[6]{1.17334}-1`
`r_{\text{Super Save}}=1.027000479-1=0.0700047876`

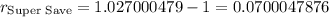
As r is represented in decimal form, the r_Super Save= 2.70%

Applying the same reasoning to Star Financial:

`r_{\text{Star Financial}}=\sqrt[3]{(2684.35)/(2500)}-1`
`r_{\text{Star Financial}}=\sqrt[3]{1.07374}-1`
`r_{\text{Star Financial}}=1.02399942-1=0.02399942017`

As r is represented in decimal form, the r_Star Financial= 2.39%

Applying the same reasoning to Better Bank:

`r_{\text{Better Bank}}=\sqrt[5]{(4525.63)/(4000)}-1`
`r_{\text{Better Bank}}=\sqrt[5]{1.1314075}-1`
`r_{\text{Better }}=1.024999871-1`
`r_{\text{Better Bank}}=0.02499987`

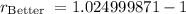
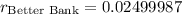
As r is represented in decimal form, the r_Better Bank= 2.49%

Now, that we have the interest rate values, we can build a table for each year corresponding to each Bank:

In order to draw the graph and using the table, we need to compute the balance for each year applying the above equation:

`\text{B}=P(1+(r)/(n))^(nt)`

Note: (Commas and periods are reversed, Spreadsheet Configuration issue)