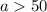Question

The function f is defined by f(x)=50⋅3x. The function g is defined by g(x)=a⋅bx. The graphs of f and g are given below. How does a, from function g(x) compare to 50 from function f(x)?

Answer 1

So, the function f is defined as:

`f(x)=50(3)^x`

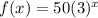
And the function g has the form:

`g(x)=a(b)^x`

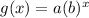
Given that the graphs of f and g are:

We could compare the value of "a" from function g(x) to 50 from function f(x) as follows:

Notice that when x=0:

`\begin{gathered} f(0)=50\cdot(3^0)=50 \\ g(0)=a\cdot(b^0)=a \end{gathered}`

As you can see from the graph, the function g is greater than the function f at the point x=0, so, comparing a with 50, we could affirm that:

`a>50`