Question

Sea Masters Co. issued $1000 par value bonds with a 9 percent coupon. The bond pays interest semi-annually and has 21 years remaining to its maturity date. If the market demands 8.5 percent required rate on the bond, what is the price of the bond? Round it two decimial places, and do not include the $ sign, e.g., 935.67.

Answer 1

The price of the bond is approximately 1,393.49.

Step-by-step explanation:

To calculate the price of the bond, you can use the present value formula for a bond. The formula is as follows:

`\[ \text{Bond Price} = \frac{\text{C} * (1 - (1 + r)^(-n))}{r} + \frac{\text{F}}{(1 + r)^n} \]`

Where:

-
`\( \text{C} \)` is the semi-annual coupon payment,

-
`\( r \)` is the semi-annual interest rate,

-
`\( n \)` is the total number of semi-annual periods,

-
`\( \text{F} \)` is the par value of the bond.

In this case:

-
`\( \text{C} = 0.09 * (\$1000)/(2) \)` (half of the annual coupon payment),

-
`\( r = 0.085 \)` (8.5% annual rate converted to semi-annual),

-
`\( n = 2 * 21 \)` (since the bond pays interest semi-annually for 21 years),

-
`\( \text{F} = \$1000 \).`

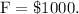
Plug these values into the formula and calculate:

`\[ \text{Bond Price} = ((0.09 * (\$1000)/(2)) * (1 - (1 + 0.085)^(-42)))/(0.085) + (\$1000)/((1 + 0.085)^(42)) \]`

The result is approximately 1,393.49.