Question

Karen obtained a $34,000 loan at 3.3% compounded semiannually. a-1. What monthly payment will repay the loan in 71/2 years? (Do not round intermediate colculotions and round your final answer to 2 decimal ploces.) Monthly payment a-2. How much interest will Karen pay over the life of the loan? (Round intermediote calculotions to 2 decimal places ond round your final answer to the nearest dollar.)

Answer 1

The monthly payment that will repay the loan in 7.5 years is approximately $434.67. Karen will pay approximately $44,240.60 in interest over the life of the loan.

Step-by-step explanation:

In order to find the monthly payment that will repay the loan in 7.5 years, we can use the formula for monthly loan payments:

`PMT = P * r * (1 + r)^n / ((1 + r)^n - 1)`

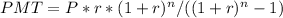
Where:
PMT = monthly payment
P = loan principal amount
r = interest rate per compounding period
n = number of compounding periods

Plugging in the given values:

P = $34,000
r = 0.033/2 = 0.0165 (semiannual interest rate)
n = 7.5 * 2 = 15 (number of compounding periods)

Solving the equation, we find that the monthly payment is approximately $434.67.

To calculate the total interest paid over the life of the loan, we can use the formula for compound interest:

Interest = Total Amount Paid - Loan Principal Amount

Plugging in the given values:

Total Amount Paid = Monthly Payment * Number of Payments
Total Amount Paid = $434.67 * 15 * 12 = $78,240.60

Interest = $78,240.60 - $34,000 = $44,240.60