In order to find the probability, first we need to calculate the triangle area and the circle area.
The triangle has a base of 8 cm and a height of 4 cm, so its area is:
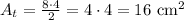
The circle has a radius of 4 cm, so:
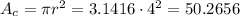
Now, to find the probability, we divide the white area (circle minus triangle) by the total area (circle):
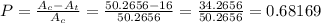
Rounding to the nearest tenth of a percent, we have a probability of 68.2%.