Question

Twenty-two athletes have gathered for a competition. Three of the athletes are infected.At the opening ceremony, they all greet each other with handshakes.i) How many handshakes are there in total?ii) What proportion of the handshakes were potentially infectious, i.e. involve a handshakebetween an infected athlete and a non-infected one.

Answer 1

For this problem, we are told that 22 athletes have gathered for a competition, where 3 athletes are infected. They all greet each other with handshakes. We need to determine how many handshakes there were and which proportion was potentially infectious.

Since the order doesn't matter here, I.e. athlete 1 handshaking athlete 2 is the same as athlete 2 handshaking athlete 1, we can use a combination of the 22 athletes taken 2 by 2. This is shown below:

`C_2^(22)=(22!)/(2!(22-2)!)=(22\cdot21\cdot20!)/(2\cdot20!)=(462)/(2)=231`

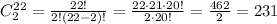
There were a total of 231 handshakes.

Now we need to determine the proportion of these that were infectious. The first step is to determine how many handshakes each infected athlete was involved in. We have:

`\text{ handshake infected}=3\cdot(21-2)=3\cdot(19)=57`

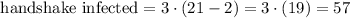
Now we need to divide the number of infected handshakes by the total number of handshakes.

`proportion=(57)/(231)=(19)/(77)`

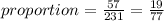
Of every 77 handshakes, 19 are infectious. Or approximately 25%.