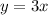Question

if "y varies directly as x", find the constant of variation and write an equation of direct variation thatrelates the two variables.1) y = 21, when x = 7

Answer 1

Given that y varies directly as x, this implies that

`y\propto x`

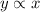
Introducing a constant of variation K, we have

`y=Kx\text{ --- equation 1}`
`when\text{ x=7, y=21}`

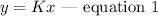
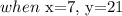
Thus, by substituting these values into equation 1, we have

`\begin{gathered} 21=3K \\ divide\text{ both sides by the coefficient of K, which is 3} \\ (21)/(3)=(3K)/(3) \\ \Rightarrow K=3 \end{gathered}`

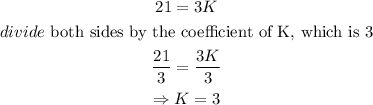
The constant of variation is

`3`

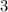
By substituting the value of K into equation 1,

we have the equation of the direct variation to be

`y=3x`