Question

Given M(5,-2) and N(-7,6), find the point P on MN such that the partitioned ratio is 1:3

Answer 1

The points we have are:

`\begin{gathered} M\mleft(5,-2\mright) \\ N\mleft(-7,6\mright) \end{gathered}`

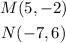
We label this points as follows for reference:

`\begin{gathered} x_1=5 \\ y_1=-2 \\ x_2=-7 \\ y_2=6 \end{gathered}`

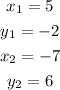
We have that the ratio is:

`1\colon3`

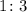
Where we will call a=1 and b=3.

And we use the following formula for finding the coordinates of a point given the two endpoints and the ratio:

`(\frac{bx_1+a_{}x_2}{a+b},(by_1+ay_2)/(a+b))`

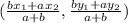
Substituting our values:

`((3(5)+1(-7))/(1+3),(3(-2)+1(6))/(1+3))`

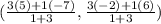
We solve the operations:

`((15-7)/(4),(-6+6)/(4))`
`\begin{gathered} ((8)/(4),(0)/(4)) \\ (2,0) \end{gathered}`

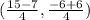
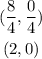
Point P is at (2,0)