First, we have to find the volume of each figure.
Sphere.

Cylinder #1.

Cylinder #2.
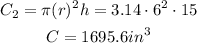
Cone #1.
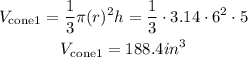
Cone #2.
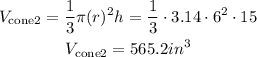
Part A: So, according to these volumes, the sphere and Cylinder 2 are the only figures with a volume greater than 600 cubic inches.
Part B.
Let's divide the volume of the sphere by the volume of Cone #1.
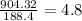
Hence, the volume of the sphere is 4.8 times greater than the volume of Cone #1.