To answer this question we will use the following two points formula to compute the equation of a line that passes through two given points:
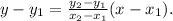
From the given table we get that the graph of the given linear function passes through (1,-5) and (2,-8) then its equation is:
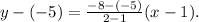
Simplifying the above result we get:
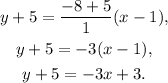
Subtracting 5 from the above result we get:
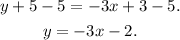
Answer:
