Step-by-step explanation
From the statement, we know that:
• the ladder reaches an electric box 31 ft up,
,
• the ladder makes an angle of 63° with the ground.
Using these data, we make the following diagram:
From the diagram, we see that the ladder and the wall form a right triangle with:
• H = hypotenuse = length of the ladder,
,
• OS = opposite side to angle θ = 31 ft,
,
• θ = angle between the ladder and the ground = 63°,
From trigonometry, we have the following trigonometric relation between H, OS and θ:
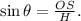
Replacing the data from above and solving for H, we get:

Answer
The length of the ladder is 34.79 ft to the nearest hundred.