The given problem can be modeled as a Binomial distribution since the following conditions are satisfied.
There are only two possible outcomes either you get a 2 or you dont.
The number of trials is fixed. (n = 4)
The probability of success is fixed.
The probability of success is the probability of getting a 2 that is 1/6
The Binomial distribution is given by

Where n is the number of trials that is 4
x is the outcome of interest which means getting a 2.
At least three 2's means three or more than three.
So, x = 3, 4
nCx is the number of possible combinations
So, this means that we have to find
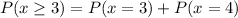
P(x = 3):
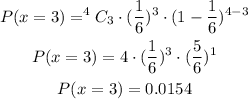
P(x = 4):
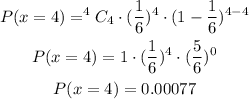
So, the probability of obtaining at least three 2's is

Therefore, the probability of obtaining at least three 2's is 0.01617