Question

Solve by using quadratic formula.x2 + 10x – 2 = 0Choices are1:x={-10.20,0.40}2:x={0.20,-15}3:x={0.20,-10.20}4:x={0.30,-10}

Answer 1

Given

`x^2+10x-2=0`

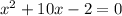
You have to determine both possible values of x by using the quadratic formula, which is:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Where

a is the coefficient that multiplies the quadratic term of the quadratic expression

b is the coefficient of the x term

c is the constant

For the given expression, the values of the coefficients are:

a=1

b=10

c=-2

Replace said coefficients in the formula and solve

`\begin{gathered} x=\frac{-10\pm\sqrt[]{10^2-4\cdot1\cdot(-2)}}{2\cdot1} \\ x=\frac{-10\pm\sqrt[]{100+8}}{2} \\ x=\frac{-10\pm\sqrt[]{108}}{2} \end{gathered}`

Now you have to solve the addition and subtraction separately

Addition

`\begin{gathered} x=\frac{-10+\sqrt[]{108}}{2} \\ x=0.196 \\ x\approx0.2 \end{gathered}`

Subtraction

`\begin{gathered} x=\frac{-10-\sqrt[]{108}}{2} \\ x=-10.196 \\ x\approx-10.20 \end{gathered}`

The possible values of x are -10.20 and 0.20.