Question

Standing on a bridge, you throw a stone straight upward. The stone hits a stream, 40.8 m below the point atwhich you release it, 3.80 s later. What is the speed of the stone (in m/s) just before it hits the water? Pleasedo not include any units in your answer below. Type in only the numerical result. If you include units, youranswer will be marked as incorrect.

Answer 1

speed = 7.88 m/s

Step-by-step explanation:

First, we need to find the initial velocity of the stone, so we will use the following equation:

`\Delta x=v_0t-(1)/(2)gt^2_{}`

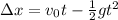
Where Δx is the distance, t is the time, v0 is the initial velocity, and g is the gravity. So, solving for v0, we get:

`\begin{gathered} \Delta x+(1)/(2)gt^2=v_0t \\ (\Delta x+(1)/(2)gt^2)/(t)=v_0 \end{gathered}`

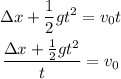
Now, replacing the values, we get;

`\begin{gathered} \frac{40.8\text{ m +}(1)/(2)(9.8m/s^2)(3.8s)^2}{3.8s}=v_0 \\ \frac{40.8\text{ m +}(1)/(2)(9.8m/s^2)(14.44s^2)}{3.8s}=v_0 \\ \frac{40.8\text{ m +70.756 m}^{}}{3.8s}=v_0 \\ \frac{111.556\text{ m}}{3.8\text{ s}}=v_0 \\ 29.36m/s=v_0 \end{gathered}`

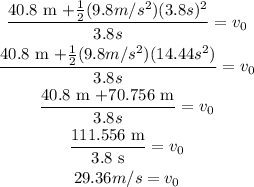
Then, the velocity of the stone just before it hits the water can be found using the following equation:

`\begin{gathered} v_f=v_0-gt \\ v_f=29.36m/s-9.8m/s^2(3.8s) \\ v_f=29.36\text{ m/s - 37.24 m/s} \\ v_f=-7.88\text{ m/s} \end{gathered}`

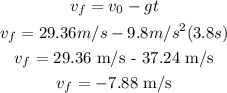
Therefore, the speed of the stone is 7.88 m/s