Question

Jane rides a sled down a slope of angle θ at constant speed v. Determine the coefficient of kinetic friction between the sled and the slope. Neglect air resistance.

A. u = g * sin(θ)
B. u = m * g * cos(θ)
C. u = tan(θ)
D. u = g * cos(θ)

Answer 1

The coefficient of kinetic friction between the sled and the slope is u = tan(θ)..Thus, the correct answer is C. u = tan(θ).

Step-by-step explanation:

In this scenario, the sled is moving at a constant speed down a slope, indicating a dynamic equilibrium between the gravitational force pulling the sled downhill and the frictional force opposing its motion. The frictional force can be expressed as:

`\(f_{\text{friction}} = \mu \cdot N\)`, where N is the normal force perpendicular to the slope.

Considering the forces parallel and perpendicular to the slope, we can express the gravitational force components as mg.sin (θ) downhill and mg.cos(θ) perpendicular to the slope.

Since the sled is moving at constant speed, the frictional force equals the component pulling it downhill, leading to the equation:

`\(f_{\text{friction}} = mg \cdot \sin`(θ) =
`\mu \cdot mg \cdot \cos\).`(θ)

Solving for the coefficient of kinetic friction:

`(\(\mu\)),` we get, g.sin(θ) / g.cos(θ)

which simplifies to
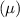`(\(\mu\))` = tan(θ). Therefore, the correct expression for the coefficient of kinetic friction is C. u = tan(θ).

This result aligns with the understanding that the coefficient of kinetic friction is the tangent of the angle of the slope. It is essential to grasp the relationship between the forces involved and apply the appropriate trigonometric functions to derive the correct expression for the coefficient of kinetic friction in the given scenario.

Full Question:

Jane rides a sled down a slope of angle θ at constant speed v. Determine the coefficient of kinetic friction between the sled and the slope. Neglect air resistance.see the picture.

A. u = g * sin(θ)

B. u = m * g * cos(θ)

C. u = tan(θ)

D. u = g * cos(θ)