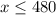Question

A shipping container will be used to transport several 40-kilogram crates across the country by rail. The greatest weight that can be loaded into the container is 25000 kilograms. Other shipments weighing 5800 kilograms have already been loaded into the container. Write and solve an inequality which can be used to determine x, the number of 40-kilogram crates that can be loaded into the shipping container.

Answer 1

Given:

40kg crates to be loaded on a shipping container which can load a maximum of 25,000kg.

The container already has 5800kg of other shipments loaded on it.

Each crate weighs 40kg

The number of 40kg crates is represented by x.

Hence, the total weight of the crates to be loaded is;

`40* x=40x\text{ kilograms}`

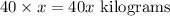
The inequality can be given by;

`\begin{gathered} 40x+5800\le25000 \\ \text{This is because the total that can be loaded on the container can not exc}eed\text{ 25000} \end{gathered}`

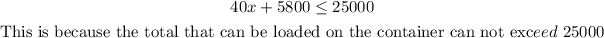
Therefore, the inequality is;

`40x+5800\le25000`

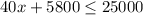
To solve for the number of crates;

`\begin{gathered} 40x+5800\le25000 \\ 40x\le25000-5800 \\ 40x\le19200 \\ \text{Dividing both sides by 40,} \\ x\le(19200)/(40) \\ x\le480 \end{gathered}`

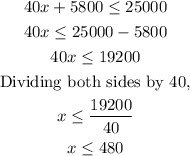
Therefore, the number of 40kg crates that can be loaded into the shipping container can not exceed 480 crates.

Hence, a maximum of 480 40kilogram crates can be loaded on the shipping container alongside other shipments weighing 5800kg.

Thus, the inequality to determine the number of 40kg crates is;

`x\le480`