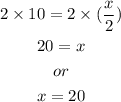Let's use a diagram:
Using the definition of tangent function:
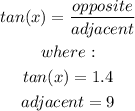
Solve for opposite:
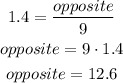
Answer:
12.6
--------------
Example:
We have to following equation:
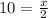
And we need to find the value of x. In order to find x, we need to isolate the variable x, we can do this using the equality property of multiplication which states: if we multiply both sides of an equation by the same number, the two sides remain equal. So:
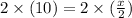
For the right hand side we can see:
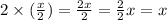
2/2 = 1 because a number divided by itself is always 1. Therefore: