Question

This is a question from my math homework in algebra 2

Answer 1

The given function is,

`y=A\cos (Bx)+C`

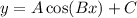
The curve passes through the point (0,8), (60,78) and (120,8).

Substituting the point (0,8) in the given equation,

`\begin{gathered} 8=A\cos (B*0)+C \\ 8=A+C\ldots\ldots\mathrm{}(1) \end{gathered}`

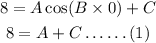
Substituting the value (60, 78) in the given equation,

`78=A\cos (60B)+C\ldots\ldots\ldots\text{.}(2)`

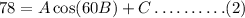
Substituting the value (120,8) in the given equation,

`8=A\cos (120B)+C\ldots\ldots\ldots\text{.}(3)`

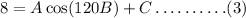
Substracting equation (3) from equation (1),

`\begin{gathered} A+C-(A\cos 120B+C)=0 \\ A(1-\cos 120B)=0 \\ A=0\text{ or cos120B=0} \\ A=0\text{ or 120B=}(\pi)/(2) \\ A=0\text{ or B=}(\pi)/(240) \end{gathered}`

The value of A cannot be zero as the curvature won't be of the cosine.

Thus, the value of B will be pi/240.

Substituting the value of B in the equation (2),

`\begin{gathered} 78=A\cos (60*(\pi)/(240))+C \\ \\ 78=0.707A+C\ldots\ldots(4) \end{gathered}`

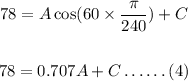
Substracting equation (4) from (1),

`\begin{gathered} 0.29A=70 \\ A=238.99 \end{gathered}`

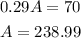
Substituting the value of A in the equation (1),

`\begin{gathered} 238.99+C=8 \\ C=230.99 \end{gathered}`

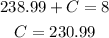
Thus, the required value of A is 238.99, the value of B is pi/240 and the value of C is 230.99.