Question

The graph of a sinusoidal function has a minimum point at (0,2) and a max point at (3pi,6) Write the formula of the function in terms of f(x), x must be in radians

Answer 1

f(x) = 2 cos ( x + π) + 4

Step-by-step explanation:

The function contains the point (0,2 ). This tells us that the sinusoidal function is cosine. (the cosine function is non-zero at x = 0).

Now, the general form of a sinusoidal we assume is

`f(x)=a\cos (x+b)+c_{}`

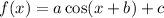
where a = amplitude

b = horizontal shift

c = vertical shift.

Let us first find the amplitude.

We know that

Max: (3pi, 6)

Min: (0 2)

This tells us that the distance from max to min is 6 - 2 = 4.

Now, this distance is 2 times the amplitude; therefore,

`\begin{gathered} 2a=4 \\ a=2 \end{gathered}`

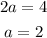
Hence, our function thus far is

`f(x)=2\cos (x+b)+c_{}`

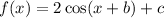
Next, let us find the vertical shift.

To find the vertical shift, a sketch will help.

The y-coordinate of the red line is where our function is centred.

Now, what is the distance to this red line from the origin?

As can be seen from the sketch, the distance is 2 + 2 = 4; therefore,

c = 4.

Therefore, the function takes the following form.

`f(x)=2\cos (x+b)+4`

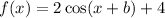
Last but not least we find b.

If b were zero then the function would have a maximum at x = 0. Instead, we are told that x = 0 is a minimum. This tells us that the function is shifted horizontally. By how much though?

By how much do we need to shift a sinusoidal function so that a minimum takes the seat of a maximum function, i.e the trough becomes the crest? The answer is by period / 2.

The period of our sinusoidal function is 2π.

Therefore, the function is shifted by π.

Hence, b = π.

Therefore, the final form of our function is

`\boxed{f(x)=2\cos (x+\pi)+4.}`