Question

I don’t know how to do this properly like I got an answer but I don’t know if it’s right

Answer 1

To calculate this, we will use the chemical equations as math equations and add them.

Firtly, we want the equation for the formation of CH₃CHO(g), so this will be the only product.

The reactants must be only the elements in their standard form, so C(g), O₂(g) and H₂(g). I would be more correct to use C(s), but since we odn't have information for this, we will assume it wants with C(g).

So, the reaction we want is:

`C(g)+O_2(g)+H_2(g)\to CH_3CHO(g)`

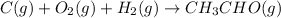
To balance the reaction, we can just do for eqach element separately, maintaining the coefficient of 1 on CH₃CHO(g):

`\begin{gathered} 2C(g)+(1)/(2)O_2(g)+2H_2(g)\to CH_3CHO\mleft(g\mright) \\ \Delta H=? \end{gathered}`

Now, we want to get to this equation adding the equations we want. We will apply the same operations to the enthalpies to get the enthalpy of formation.

The first given equation has the CH₃CHO(g), but it is on the left side and with coefficient of 2, so we need to invert the reaction and divided every coefficient by 2. The same operations have to be applied to the enthalpy, so the sign of the enthalpy will invert and it will be divided by 2:

`\begin{gathered} 2CO_2(g)+2H_2O(l)\to CH_3CHO(g)+(5)/(2)O_2(g)_{} \\ \Delta H=(2308.4kJ)/(2)=1154.2kJ \end{gathered}`

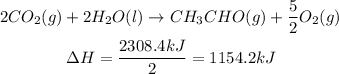
The second given equation has both C(g) and O₂(g), but since the third equation also has O₂(g), we will look just for C(g). We need 2 C(g), so we will need to doulbe the equation and its enthalpy:

`\begin{gathered} 2C(g)+2O_2(g)\to2CO_2(g) \\ \Delta H=2\cdot-414.0kJ=-828.0kJ \end{gathered}`

For the last, we will look into H₂(g) and since all the equations are balanced, O₂(g) will also be balanced by the end of it.

We need 2 H₂(g), so we don't need to do anything with this reaction:

`\begin{gathered} 2H_2(g)+O_2(g)\to H_2O(l) \\ \Delta H=-597.4kJ \end{gathered}`

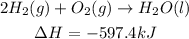
Now, we add the equations:

`\begin{gathered} \cancel{2CO_2\mleft(g\mright)}+\cancel{2H_2O\mleft(l\mright)}\to CH_3CHO(g)+\cancel{(5)/(2)O_2(g)}_{} \\ 2C(g)+\cancel{2O_2(g)}\to\cancel{2CO_2(g)} \\ 2H_2(g)+\cancel{O_2(g)}\to\cancel{H_2O(l)} \\ ------------------------------- \\ 2C(g)+(1)/(2)O_2(g)+2H_2(g)\to CH_3CHO(g) \end{gathered}`

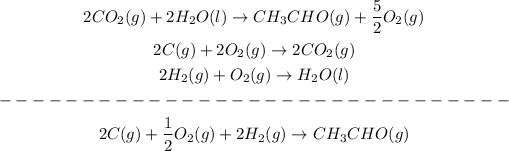
And we do the same with the enthalpies:

`\begin{gathered} \Delta H=1154.2kJ+(-828.0kJ)+(-597.4kJ) \\ \Delta H=1154.2kJ-828.0kJ-597.4kJ \\ \Delta H=-271.2kJ \end{gathered}`

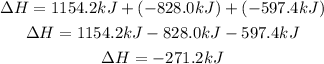
This is the enthalpy for this reaction. To get the molar enthalpy of formation, we need to divide this value by the coefficient of CH₃CHO(g). Since this coefficient is 1, we have:

`\Delta H_m=-(271.2kJ)/(1mol)=-271.2kJ\/mol`

So, the molar enthalpy of formation given the data is -271.2 kJ/mol.