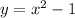Question

I have been given ordered pairs. I have graphed them. It is a nonlinear function. I know x increases by 1. Does y increase by 1, 2, 3 or 5? Also I need to write an equation representing this function. Please help?

Answer 1

We could analyze how each coordinate pair is increasing.

A linear function always increases or decreases at a constant rate, so, each coordinate should have the same rate between each point. This doesn't happen here. So, the function is not linear. As you can see, "y" increases by 2 more than its previous increase.

An equation for the function could be a parabola with the equation:

`y=x^2-1`

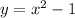
If we replace each coordinate pair in the equation, we can notice that the equation is satisfied for each one of them. Thus, that is the equation for y. :)

But.... How did we get the equation for y?

If we replace all the given points in the coordinate plane, we notice that they have he form of a parabola. Now, since (0,-1) is the minimum point of the graph (That's the lower point of all given points) we could suppose that it is the vertex of the parabola.

Using the fact that a parabola has the general form:

`y=a(x-h)^2+k`

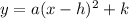
Where (h,k) is the vertex, we could replace these values and a point to find the value of a:

`\begin{gathered} C(h,k)=C(0,-1) \\ y=a(x-h)^2+k\to y=a(x-0)^2-1 \\ y=ax^2-1 \end{gathered}`

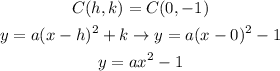
Now, we could replace any point that we want. It could be (2,3) for example. Here, x=2 and y=3. So,

`\begin{gathered} 3=a(2)^2-1 \\ 4=4a \\ a=1 \end{gathered}`

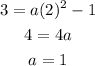
Thus,

`y=a(x-h)^2+k\to y=1(x-0)^2-1`

And, this is the same to write:

`y=x^2-1`