Question

Hello, I need some assistance with this homework question please for precalculusHW Q35

Answer 1

The given polynomial function is:

`f(x)=-2(x-1)(x+3)^2`

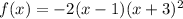
a. Find any real zeros of f.

To find the real zeros, we need to find the x-values that make each of the factors equal to zero, so, the factors of the polynomial function are:

`\begin{gathered} -2 \\ (x-1) \\ (x+3)^2 \end{gathered}`

Equal (x-1) and (x+3) to zero and solve for x:

`\begin{gathered} x-1=0 \\ x=1\text{ Real zero} \\ x+3=0 \\ x=-3\text{ Real zero} \end{gathered}`

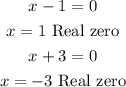
The real zeros of f are 1,-3

The multiplicity is given by the power of the factor, then 1 has multiplicity 1 and -3 has multiplicity 2, so:

The multiplicit of the larger zero is 1

The multiplicity of the smaller zero is 2

b. Determine whether the graph crosses or touches the x-axis at each x-intercept.

When multiplicity is even the graph touches the x-axis and when is odd the graph crosses the x-axis.

Then, the graph crosses the x-axis at the larger x-intercept.

The graph touches the x-axis at the smaller x-intercept.

c. The maximum number of turning points is determined by the degree of the polynomial, we can rewrite the polynomial as:

`\begin{gathered} f(x)=(-2x+2)(x+3)^2 \\ f(x)=(-2x+2)(x^2+2*3*x+3^2) \\ f(x)=(-2x+2)(x^2+6x+9) \\ f(x)=-2x*x^2-2x*6x-2x*9+2x^2+2*6x+2*9 \\ f(x)=-2x^3-12x^2-18x+2x^2+12x+18 \\ f(x)=-2x^3-10x^2-6x+18 \end{gathered}`

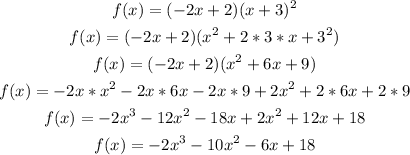
The degree (n) is the greatest power, then this polynomial is degree n=3, and the number of turning points is given by n-1, so:

The maximum number of turning points on the graph is 2

d. Type the power function that the graph of f resembles for large values of |x|

We can apply the end behavior theorem which states: for larger values of |x| the graph of the polynomial:

`f(x)=a_nx^n+a_(n-1)x^(n-1)+...+a_1x+a_0`

resembles the graph of the power function:

`y=a_nx^n`

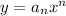
Thus, the power function that the graph of f resembles for larger values of |x| is:

`y=-2x^3`