Shaded region =20.75
Step-by-step explanation
The area of a circle can be calculated using the formula below:
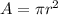
where A is the area of the circle.
r is the radius of the sircle
π is a constant.
The area of a rectangle is given by the formula;
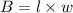
where B is the area of the rectangle
l is the length of the reactangle.
w is width (height) of the rectangle.
From the given diagram;
d = 10 but r = d/2 = 10/2 = 5
π = 3.14
l= 10
w=6
There are two shapes in the given figure. To find the shaded region, we need to find area of the circle and then area of the rectangle, we then subtract half of the area of the circle from area of the rectangle.
Substitute values into the area of circle and evaluate.
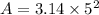
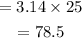
A = 78.5
Half of area of the circle = 39.25
Next, substitute values into the rectangle formula and evaluate.
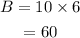
Shaded region = Area of rectangle - Half area of a circle
= 60 - 39.25
Shaded region = 20.75