Question

Of the teenager surveyed, 46% on a game console, 35% own a personal computer, And 29% owns both a game console and personal computer. What is the conditional probability that a teenager randomly selected owns a game console, given that the teenager owns a personal computer?

Answer 1

Given:

Teenagers who own a game console = 46%

Teenagers who own a personal computer = 35%

Teenagers who own both a game console and personal computer = 29%

Required- the conditional probability that a teenager randomly selected owns a game console, given that the teenager owns a personal computer.

Step-by-step explanation:

Let A be the event that the teenager randomly selected owns a game console.

Let B be the event the teenager randomly selected owns a personal computer.

Now, we change the probability of each event in decimal as:

`\begin{gathered} P(A)=46\% \\ \\ =(46)/(100) \\ \\ =0.46 \end{gathered}`

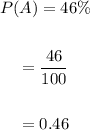
Now, the probability of event B is:

`\begin{gathered} P(B)=35\% \\ \\ =(35)/(100) \\ \\ =0.35 \end{gathered}`

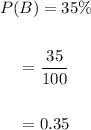
Now, the probability of events A and B is:

`\begin{gathered} P(A\text{ and B})=29\% \\ \\ =(29)/(100) \\ \\ =0.29 \end{gathered}`

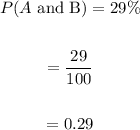
We know that the formula to find the conditional probability of event A, given event B is:

`P(A|B)=\frac{P(A\text{ and B})}{P(B)}`

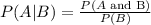
Now, we put the given values in the formula, we get:

`\begin{gathered} P(A|B)=(0.29)/(0.35) \\ \\ =0.82857 \\ \\ \approx0.83 \end{gathered}`

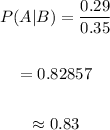
Final answer: The conditional probability that a teenager randomly selected owns a game console, given that the teenager owns a personal computer is approximately 0.83.