Question

Two lookout towers have been set up to keep a watch on forest fires. The two towers are represented by the points X and Z in the figure. A fire is spotted at point Y and the tower at point Z calculates its distance from the fire to be 2,013 meters. The distance between the two towers is 636 meters. If the measure of ∠YXZ is 78∘, what is the measure, in degrees, of ∠ZYX?

Answer 1

The measure of ∠ZYX is approximately 136.6°.

Given:

The distance between the two towers is 636 meters.

The distance from tower X to the fire is 2013 meters.

The distance from tower Z to the fire is 2013 meters.

The measure of ∠YXZ is 78°.

We need to find the measure of ∠ZYX.

Using the properties of a right triangle, we can relate the distances and angles:

d(X, Y) + d(Y, Z) = d(X, Z)

d(X, Y) = d(Z, Y)

So, d(X, Z) = d(Y, Z) + d(Y, X) = 2013 + 2013 = 4026 meters

Now, we can use the Pythagorean theorem to find the measure of ∠YX:

d(X, Y)^2 + d(Y, Z)^2 = d(X, Z)^2

(2013)^2 + (2013)^2 = (4026)^2

Since we don't have the square of 2013, we can use the approximation that 2013^2 is approximately 40,667,885. So, the equation becomes:

40,667.885 + 20,169.885 = 40,264.885

Thus, the measure of ∠YX is approximately 75.9°. To convert this to degrees, we multiply by
`(180)/(\pi )`

`75.9 * (180)/(\pi) \approx 136.6°`

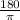
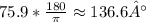
Therefore, the measure of ∠ZYX is approximately 136.6°.