Question

Not sure on how to do this. Could really use some help. (It says there is 2 parts to the question not sure if there is but I’m assuming it’s after the 1st part is answered.)

Answer 1

Step-by-step explanation

Part 1

The cone shown is oblique. The formula to find the volume of an oblique cone and a right cone is the same. That formula is:

`\begin{gathered} V=(1)/(3)\pi r^2h \\ \text{ Where} \\ V\text{ is the volume} \\ r\text{ is the radius of the base} \\ h\text{ is the height} \end{gathered}`

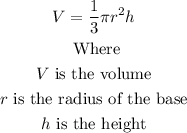
In this case, we have:

`\begin{gathered} r=\frac{\text{ Diameter}}{2}=(10ft)/(2)=5ft \\ h=3ft \end{gathered}`
`\begin{gathered} V=(1)/(3)\pi r^2h \\ V=(1)/(3)\pi(5ft)^2(3ft) \\ V=(1)/(3)\pi(25ft^2)(3ft) \\ V=\pi(25ft^3) \\ V=25\pi ft^3 \end{gathered}`

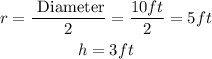
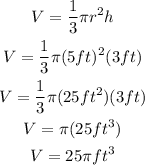
Part 2

Using a calculator, we multiply 25 by π and round to the nearest whole number.

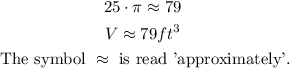
`\begin{gathered} 25\cdot\pi\approx79 \\ V\approx79ft^3 \\ \text{ The symbol }\approx\text{ is read 'approximately'.} \end{gathered}`Answer

Part 1. The volume of the cone in terms of π is 25π cubic ft.

Part 2. The volume rounded to the nearest cubic foot is about 79 cubic ft.