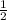Question

The stem-and-leaf plot shows the cost of lamps at a department store. 1 2 2 5 LO 8 Noo 3 0 2 4 4 9 LETO 5 6 8 8 9 6 5 5 59 7 5 8 Key: 30 means $30 (a) What is the median cost? (b) Is there a mode? If so, what is it? (c) What is the difference between the most expensive and least expensive lamps? (d) How many lamps cost more than $20 but less than $40? (e) What is the ratio of lamps that cost less than $40 to lamps that cost more than $40? Write the ratio in simplest

Answer 1

Given Stem-and-Leaf Plot, you know that:

`3|0=\text{ \$}30`

That means that Stem 3, Leaf 0, means $30.

Knowing the above, you can list all the values given in the Stem-and-Leaf Plot:

`12,25,28,30,32,34,49,56,58,58,59,60,65,65,65,69,75,78`

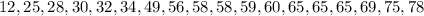
(a) By definition, the Median is the middle value of the data set.

In order to find the Median, you can follow these steps:

1. In this case, you already have the values written in ascending order (from the least value to the greatest value).

2. Identify the number of values in the list:

`n=18`

3. Since there are an even number of values, the Median will be the average of the middle two numbers:

`\begin{gathered} Median=(58+58)/(2) \\ \\ Median=58 \end{gathered}`

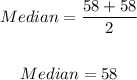
(b) By definition, the Mode is the value of the data set that appears most often. In this case, you can identify that this is:

`Mode=65`

(c) Observe that the cost of the most expensive lamp is $78, and the cost of the least expensive lamp is $12.

Therefore, you need to subtract the cost of the least expensive lamp from the cost of the most expensive lamp, in order to find the Difference in their cost:

`\text{ \$}78-\text{\$}12=\text{\$}66`

(d) Notice that the costs greater than $20 are:

`25,28,30,32,34,49,56,58,58,59,60,65,65,65,69,75,78`

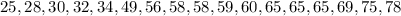
And the costs less than $40:

`12,25,28,30,32,34`

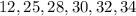
Therefore, you can conclude that the costs greater than $20 but less than $40 are:

`25,28,30,32,34`

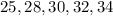
That corresponds to 5 lamps.

(e) Notice that there are 6 lamps that cost less than $40, and there are 12 lamps that cost more than $40. Therefore, the ratio is:

`ratio=(6)/(12)=(1)/(2)`

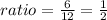
Hence, the answers are:

(a)

`Median=58`

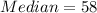
(b) Yes, there is a Mode:

`Mode=65`

(c) Difference:

`\text{\$}66`

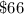
(d) Five (5) lamps.

(e) Ratio:

`(1)/(2)`