Question

In the diagram below of triangle NPQ, R is a midpoint of NP and S is a midpoint of PQ. If RS = 23 - x, and NQ = 2x + 18, what is the measure of NQ?

Answer 1

The measure of NQ is 32 units.

Step-by-step explanation:

Given that R is a midpoint of NP and S is a midpoint of PQ, the by the Midpoint Theorem for Triangles, we have:

`RS=(1)/(2)* NQ`

Substituting the given expressions, we have:

`\begin{gathered} 23-x=(1)/(2)(2x+18) \\ 2(23-x)=2x+18 \end{gathered}`

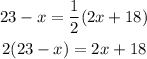
Next, solve for x:

`\begin{gathered} 46-2x=2x+18 \\ 46-18=2x+2x \\ 28=4x \\ x=(28)/(4) \\ x=7 \end{gathered}`

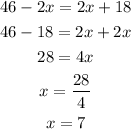
Thus, the measure of NQ will then be:

`\begin{gathered} NQ=2x+18 \\ =2(7)+18 \\ =14+18 \\ =32\text{ units} \end{gathered}`

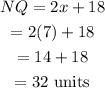
The measure of NQ is 32 units.