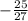Question

Find the second derivative at (4,3)X^2+y^2=25

Answer 1

Given the equation:

`x^2+y^2=25`

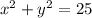
Let's find the second derivative at the point (4, 3).

Subtract 25 from both sides to equate to zero

`\begin{gathered} x^2+y^2-25=25-25 \\ \\ x^2+y^2-25=0 \end{gathered}`

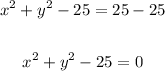
To find the second derivative, first find the first derivative:

`\begin{gathered} 2x+2y(dy)/(dx)=0 \\ \\ (dy)/(dx)=-(x)/(y) \end{gathered}`

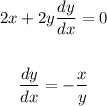
Now find the second derivative:

`\begin{gathered} (d^2y)/(dx^2)=-(x^(\prime)(y)-xy^(\prime))/(y^2) \\ \\ (d^2y)/(dx^2)=-(y-x(dy)/(dx))/(y^2) \end{gathered}`

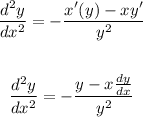
Now, pulg in 4 for x and 3 for y:

dy/dx = -4/3

`\begin{gathered} (d^2y)/(dx^2)=-(3-4(-(4)/(3)))/(3^2) \\ \\ (d^(2)y)/(dx^(2))=-(9+16)/(27)=-(25)/(27) \end{gathered}`

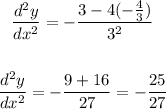
ANSWER:

`-(25)/(27)`