Question

Consider the two equations below: Equation A: 4x - 2y = -6 Equation B: 3x +y = 3 Write each equation in slope-intercept form and select which of the following statements is true.A.The slopes of both lines are the same and the y-intercepts are different. B.The slopes of both lines are different but the y-intercepts are the same. C.The slopes and y-intercepts of both lines are the same. D.The slopes and y-intercepts of both lines are different

Answer 1

B.The slopes of both lines are different but the y-intercepts are the same.

Step-by-step explanation:

The slope-intercept form of the equation of a line is:

`y=mx+b`

First, make the subject of equations A and B y.

Equation A:

`\begin{gathered} 4x-2y=-6 \\ 2y=4x+6 \\ y=(4x)/(2)+(6)/(2) \\ y=2x+3 \end{gathered}`

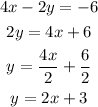
Equation B:

`\begin{gathered} 3x+y=3 \\ y=-3x+3 \end{gathered}`

Thus:

• The slope of Equation A is 2 while the y-intercept is 3.

,

• The slope of Equation B is -3 while the y-intercept is 3.

The slopes of both lines are different but the y-intercepts are the same.

The correct choice is B.