Question

What is the partial fraction​ decomposition of 4x+18/x^3-x^2-6x

Answer 1

The partial fraction decomposition would have the form

`\[ (4x + 18)/(x(x - 3)(x + 2)) = (A)/(x) + (B)/(x - 3) + (C)/(x + 2) \]`

Explanation:

The given rational function can be expressed as

`\[ (4x + 18)/(x^3 - x^2 - 6x) \]`

we can factor the denominator

`x^3 - x^2 - 6x` =
`x(x^2 - x - 6)`

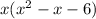
Factoring the quadratic term in the parentheses

x(x^2 - x - 6) = x(x - 3)(x + 2)

So, the partial fraction decomposition would have the form

`\[ (4x + 18)/(x(x - 3)(x + 2)) = (A)/(x) + (B)/(x - 3) + (C)/(x + 2) \]`