we know the equation of radiactive decreasing is:
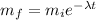
where mf is the final concentration (40 and 90 bq/L) mi is the initial concentration (161 and 186 bq/L), lamda is the decreacion constant of each element and t is the time, so we replace the information and solve the equation for t:
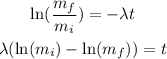
So if lamda is equal to 20 we replace:
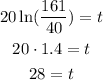
Si they have to wait 28 years