Question

How far apart are parallel lines m and n such that T0, -12.(AXYZ) = (R, Rm) (AXYZ)?Parallel lines m and n areunits apart

Answer 1

We have to find the distance between m and n, which are parallel.

The composition of a reflection over n and a reflection over m are equal to a translation of 12 units down in the y-coordinates.

This means that m and n have slope equal to 0, as the reflection does not transform the x-coordinates as well as the y-coordinates.

Then, if we define yn as the line n and ym as the line m, the first reflection would be:

`(x,y)\longrightarrow(x,2\cdot y_n-y)`

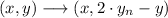
Then, we apply the reflection over m and we get:

`(x,2y_n-y)\longrightarrow(x,2y_m-(2y_n-y))=(x,2y_m-2y_n+y)=(x,y-12)`

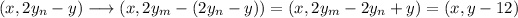
Then, we can write:

`\begin{gathered} 2y_m-2y_n=-12 \\ 2(y_m-y_n)=-12 \\ y_m-y_n=-6 \end{gathered}`

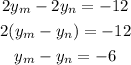
As the difference between m and n is -6, the distance between them is the absolute value of this difference:

`D=|y_m-y_n|=|-6|=6`

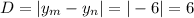
Parallel lines m and n are 6 units apart.